Loading... 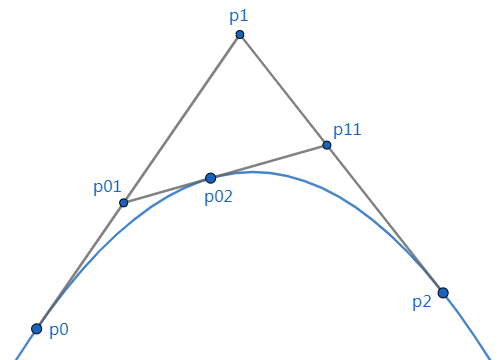 <ggb-content file="https://www.cheapface.top/ggbContents/抛物线3切线.ggb" height="600"></ggb-content> 如上图所示,已知: ${1.}$ 抛物线的一般形式为:$y = ax^2 + bx + c $ ${2.}$ $p_{0}$ 和 $p_{2}$ 是抛物线上不相同的两点,过这两点分别作切线,交于点 $p_{1}$ ${3.}$ $p_{02}$ 是 $p_{0}$ 和 $p_{2}$ 间一点,过点 $p_{02}$ 作切线,分别交直线 $p_{0}p_{1}$ 和 $p_{1}p_{2}$ 于点 $p_{01}$ 和点 $p_{12}$ 证: $$ \frac{p_{0}p_{01}}{ p_{0}p_{1} } = \frac{p_{1}p_{12}}{p_{1}p_{2}} = \frac{p_{01}p_{02}}{p_{01} p_{12}} $$ --- 设过此抛物线上任意一点$(x_{t},y_{t})$ 的切线方程为:$y = kx + d$ 此点同时满足抛物线和切线方程,即:$ax_{t}^2 + bx_{t} + c = kx_{t} + d$ 则:$d = ax_{t}^2 + (b-k)x_{t} + c$ 对抛物线求一阶导数,得到此切线的斜率:$k = 2ax_{t} + b$ 则过点 $(x_{t},y_{t})$ 的切线可以表示为: $$ \begin{align} y = kx_{t} + d &= (2ax_{t} + b)x_{t} + ax_{t}^2 + (b-(2ax_{t} + b))x_{t} + c \\ &= (2ax_{t} + b)x_{t} - ax_{t}^2 + c\end{align} $$ 设三个切点的坐标分别为:$\begin{cases}p_{0}&:(x_{0},y_{0}) \\p_{02}&:(x_{02},y_{02}) \\p_{2}&:(x_{2},y_{2}) \end{cases}$ 则三条直线的方程即为:$\begin{cases}p_{0}p_{1}&:(2ax_{0} + b)x_{0} - ax_{0}^2 + c \\p_{01}p_{12}&:(2ax_{02} + b)x_{02} - ax_{02}^2 + c \\p_{1}p_{2}&:(2ax_{2} + b)x_{2} - ax_{2}^2 + c \end{cases}$ 对点 $p_{01}$ 分析:该点是直线 $p_{0}p_{1}$ 与直线 $p_{01}p_{12}$ 的交点,即同时满足两个直线方程: $$ \begin{align} (2ax_{0} + b)x_{01} - ax_{0}^2 + c &= (2ax_{02} + b)x_{01} - ax_{02}^2 + c \\ ( (2ax_{0} + b) - (2ax_{02} + b))x_{01} &= a(x_{0}^2 - x_{02}^2) \\2a(x_{0} - x_{02})x_{01} &= a(x_{0} + x_{02})(x_{0} - x_{02}) \\2x_{01} &= x_{0} + x_{02} \\x_{01} &= \frac{x_{0} + x_{02}}{2}\end{align} $$ 同理,对点 $p_{1}$ 和 $p_{12}$ 分析,得到 $\Large{ \begin{cases}x_{1} &= \frac{x_{0} + x_{2}}{2} \\x_{11} &= \frac{x_{02} + x_{2}}{2}\end{cases}}$ 则: $$ \Large{ \begin{cases}\frac{p_{0}p_{01}}{p_{0}p_{1}} &= \frac{x_{01} - x_{0}}{x_{1} - x_{0} } &= \frac{\frac{x_{0} + x_{02}}{2} - x_{0}}{\frac{x_{0} + x_{2}}{2} - x_{0} } &= \frac{x_{02} - x_{0} }{x_{2} - x_{0} } \\\frac{p_{1}p_{12}}{p_{1}p_{2}} &= \frac{x_{11} - x_{1}}{x_{2} - x_{1} } &= \frac{\frac{x_{02} + x_{2}}{2} - \frac{x_{0} + x_{2}}{2}}{x_{2} -\frac{x_{0} + x_{2}}{2} } &= \frac{x_{02} - x_{0} }{x_{2} - x_{0} } \\\frac{p_{01}p_{02}}{p_{01} p_{12}} &= \frac{x_{02} - x_{01}}{x_{11} - x_{01} } &= \frac{x_{02} - \frac{x_{0} + x_{02}}{2}}{\frac{x_{02} + x_{2}}{2} -\frac{x_{0} + x_{02}}{2} } &= \frac{x_{02} - x_{0} }{x_{2} - x_{0} } \end{cases} } $$ 即: $$ \frac{p_{0}p_{01}}{ p_{0}p_{1} } = \frac{p_{1}p_{12}}{p_{1}p_{2}} = \frac{p_{01}p_{02}}{p_{01} p_{12}} $$ 最后修改:2021 年 05 月 20 日 © 允许规范转载 赞 2 如果觉得我的文章对你有用,请随意赞赏