Loading... 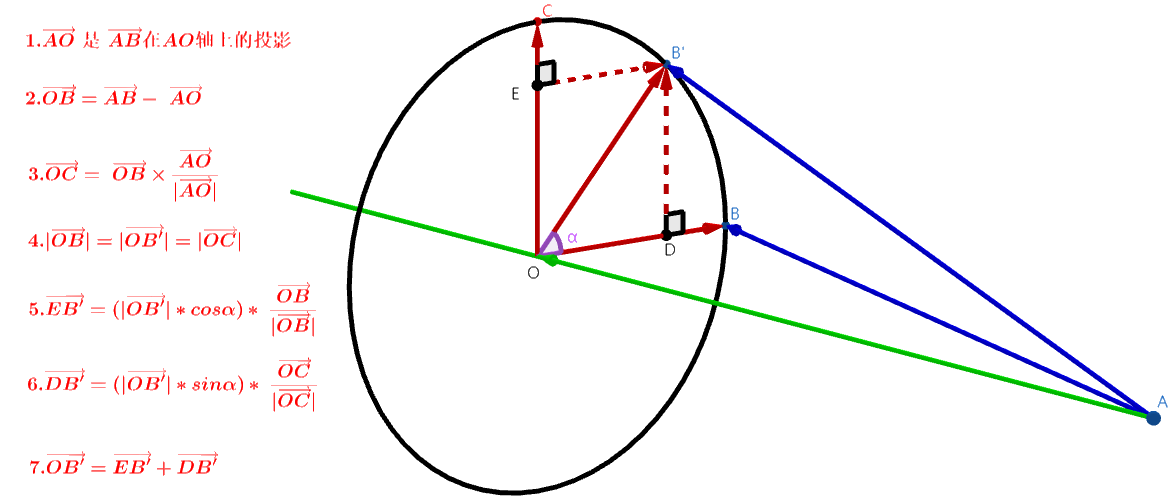 即已知向量$\vec{AB}$ 、旋转轴${AO}$以及旋转角度 $\alpha$ , 求旋转后向量$\vec{AB'}$ --- 若使用矩阵计算,一般思路为:先将旋转轴转至某一单位轴再进行旋转,之后再转回原方向。使用旋转矩阵虽然可以很方便地求出结果,但对于CPU来说,矩阵计算稍显复杂,无法利用GPU的异步多线程加速。故此处使用纯向量计算。 ${1.}$ 作$\vec{AB}$向量在旋转轴${AO}$上的投影$\vec{AO}$ ${2.}$ 利用矢量平行四边形相加法则,有:$\vec{OB} = \vec{AB} - \vec{AO}$ ${3.}$ 作$\vec{OC}$同时垂直于$\vec{AO}$和$\vec{OB}$,有:$\vec{OC} = \vec{OB} \times \frac{\vec{AO}}{|\vec{AO'}|}$,因为$\vec{AO} \bot \vec{OB}$,所以: $$ |\vec{OC}| = \frac{|\vec{AO}|}{|\vec{AO}|}*|\vec{OB}|*sin\ 90^\circ =|\vec{OB}| $$ 故点${C}$和点${B'}$以及点${B}$均在同一个圆上。由图可知,向量$\vec{OB'}$可以分解为$\vec{EB'}$和$\vec{DB'}$的矢量和 ${4.}$ 对三角形${B'BO}$分析,有: $$ \begin{cases} \vec{EB'} = (|\vec{OB}|*cos\alpha) * \frac{\vec{OB}}{|\vec{OB}|} \\ \vec{DB'} = (|\vec{OB}|*sin\alpha) * \frac{\vec{OC}}{|\vec{OC}|} \end{cases} $$ ${5.}$ 利用矢量平行四边形相加法则,有: $$ \begin{cases} \vec{OB'} =\vec{EB'} + \vec{DB'} \\ \vec{AB'} = \vec{AO} + \vec{OB'} \end{cases} $$ 向量$\vec{AB'}$即所求 最后修改:2021 年 04 月 08 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏