Loading... 在二维坐标系中,一个向量的旋转就是绕某个点的旋转,假设此点为原点,作下图: 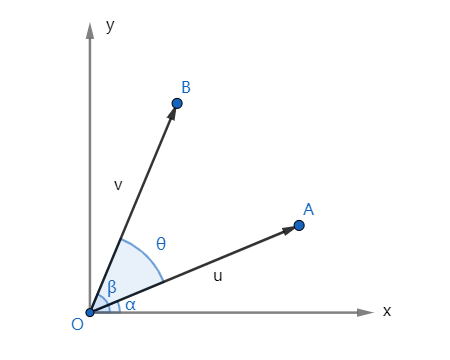 即已知向量$\vec{OA} : (x_{A},y_{A})$和旋转角度 $\theta$, 求旋转后向量$\vec{OB} : (x_{B},y_{B})$ --- 设$\vec{OA}$的长度为$r$,$\vec{OA}$和$\vec{OB}$与$x$轴的夹角分别为$\alpha$和$\beta$,则$\vec{OA}$和$\vec{OB}$的极坐标形式分别为: $\vec{OA}:(r\cos \alpha ,r\sin \alpha)$和$\vec{OB}:(r\cos \beta,r\sin \beta)$ 据图,$\beta = \alpha + \theta $,则: $$ \begin{cases} r\cos \beta &= r\cos (\alpha+\theta) &= r(cos \alpha cos \theta -sin \alpha sin \theta) &= rcos \alpha cos \theta - rsin \alpha sin \theta \\ r\sin \beta &= r\sin(\alpha+\theta) &= r(sin\alpha cos \theta +cos \alpha sin \theta) &= rsin \alpha cos \theta + rcos\alpha sin \theta \end{cases} $$ 把$\begin{cases}x_{A} &= r\cos\alpha \\y_{A} &= r\sin\alpha \\x_{B} &= r\cos\beta \\y_{B} &= r\sin\beta \end{cases}$ 带入上式,则$\begin{cases}x_{B} &= x_{A}cos\theta - y_{A}sin\theta \\y_{B} &= x_{A}sin\theta + y_{A}cos\theta \end{cases}$ 即得到从一个向量到另一个向量的线性变换。若旋转中心不为原点,先平移至原点,经过上述旋转变换后再反平移回原旋转中心 --- 此线性变换还可以表达为矩阵乘积的形式: 用一个二阶行矩阵表示向量$\vec{OA}$为:$\begin{bmatrix} x_{A} & y_{A} \end{bmatrix} $,$\vec{OB}$为$\begin{bmatrix} x_{B} & y_{B} \end{bmatrix}$ 有:$\begin{bmatrix} x_{B} & y_{B} \end{bmatrix}= \begin{bmatrix} x_{A} & y_{A} \end{bmatrix} \times \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$ 则二维向量旋转$\theta$度角的变换矩阵可以表示为:$R = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$ 若朝反方向(即顺时针)旋转,只需将$\theta$改为$-\theta$,根据正弦函数和余弦函数的奇偶性, 得到顺时针旋转的变换矩阵:$R^{-1} = \begin{bmatrix} cos\ (-\theta) & sin\ (-\theta) \\ -sin\ (-\theta)& cos\ (-\theta) \end{bmatrix} = \begin{bmatrix} cos\theta & \ -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$ 最后修改:2021 年 04 月 10 日 © 允许规范转载 赞 1 如果觉得我的文章对你有用,请随意赞赏